Introduction
The laws of planetary motion, formulated by Johannes Kepler in the early 17th century, revolutionized our understanding of the movement of celestial bodies. These laws describe the motion of planets in our solar system and have played a crucial role in the development of modern astronomy and physics. In this blog post, we will provide an overview of the laws of planetary motion and discuss their importance in our understanding of the universe.
Overview of Laws of Planetary Motion
Kepler’s laws of planetary motion consist of three fundamental principles that describe the behavior of planets orbiting the sun:
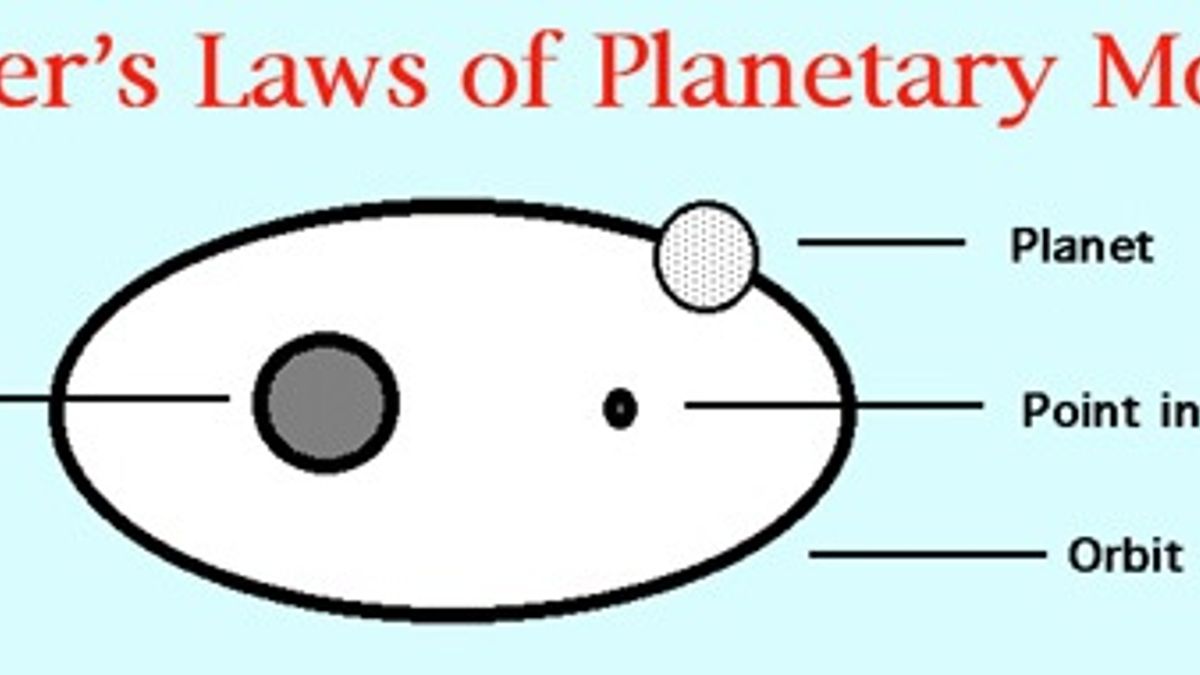
1. **First Law (Law of Ellipses):** The orbit of every planet is an ellipse with the sun at one of the two foci. In simpler terms, planets do not orbit the sun in perfect circles but follow elliptical paths, where the sun is located at one of the two foci of the ellipse.
2. **Second Law (Law of Equal Areas):** A line segment joining a planet and the sun sweeps out equal areas during equal intervals of time. This law implies that a planet moves faster when it is closer to the sun and slower when it is farther away. It also explains why planets’ speeds vary at different points in their orbit.
3. **Third Law (Harmonic Law):** The square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit. This law establishes a mathematical relationship between a planet’s orbital period and the average distance from the sun. It allows scientists to calculate the period of a planet’s orbit based on its distance from the sun or vice versa.
Importance of Understanding Planetary Motion
Understanding the laws of planetary motion is essential in various fields of study, including astronomy, astrophysics, and celestial mechanics. Here are some reasons why the knowledge of planetary motion is significant:
1. **Predicting Planetary Behavior:** Kepler’s laws allow astronomers to accurately predict the positions and movements of planets in the sky. This knowledge is essential for planning observations, designing space missions, and studying the dynamics of the solar system.
2. **Exploring the Universe:** The laws of planetary motion are not limited to our solar system but can be applied to planetary systems around other stars. By understanding how planets move in different systems, scientists can gain insights into the formation and evolution of planetary systems across the universe.
3. **Testing Newton’s Laws of Gravity:** Kepler’s laws played a crucial role in the development of Isaac Newton’s theory of gravity. By observing the deviations from Kepler’s laws, Newton was able to formulate his laws of universal gravitation, which revolutionized our understanding of the physical forces governing celestial bodies.
In conclusion, the laws of planetary motion are fundamental principles that describe the motion of planets in our solar system. They have provided a framework for understanding the behavior of planets and have been essential in the advancement of astronomy and physics. By studying these laws, scientists have been able to predict planetary behavior, explore the universe, and test our fundamental understanding of gravity.
Kepler’s Laws Explained
Kepler’s First Law: Law of Ellipses
One of Johannes Kepler’s three laws of planetary motion is the Law of Ellipses. This law states that planets move in elliptical orbits with the Sun at one of the foci. An ellipse is a closed curve in which the sum of the distances from any point on the curve to the two foci is constant. In simpler terms, the path that a planet follows around the Sun is not a perfect circle, but rather a slightly elongated or flattened shape. The Sun is located at one of the two foci of this ellipse.
Kepler’s Second Law: Law of Equal Areas
Another important law formulated by Kepler is the Law of Equal Areas. This law states that the imaginary line joining a planet and the Sun sweeps equal areas of space during equal time intervals as the planet orbits. In other words, the speed of a planet is not constant throughout its orbit. When a planet is closer to the Sun, it moves faster, and when it is farther away, it moves slower. This law helps explain the phenomenon of a planet’s varying speed during different parts of its orbit.
Kepler developed these laws based on observations made by Tycho Brahe, who meticulously recorded the positions of the planets over a long period of time. By analyzing this data, Kepler was able to deduce these fundamental principles that govern the motion of planets in our solar system. These laws provided a profound understanding of planetary motion and formed the basis for later advancements in celestial mechanics.
Kepler’s Third Law: Law of Harmonies
The third law, often referred to as the Law of Harmonies, states that a planet’s orbital period is proportional to the size of its orbit, also known as its semi-major axis. This means that planets farther from the Sun take longer to complete one orbit compared to those closer to the Sun. The precise mathematical relationship between a planet’s period and its distance from the Sun is defined by Kepler’s third law. It allows astronomers to calculate the orbital periods of planets and predict their positions in the future.
Kepler’s laws of planetary motion revolutionized our understanding of the Solar System and provided a solid foundation for Isaac Newton’s later development of the laws of universal gravitation. These laws not only explained the motion of planets but also opened up new avenues for scientific exploration and discovery. Today, we continue to use Kepler’s laws to study and understand the celestial bodies that exist in our universe.
Kepler’s Third Law: Law of Harmonies
Understanding the Relationship between Sidereal Periods and Mean Distances
One of Johannes Kepler’s most significant contributions to our understanding of planetary motion is his third law, known as the Law of Harmonies. This law states that the ratio of the squares of the periods of any two planets is equal to the ratio of the cubes of their average distances from the Sun. In simpler terms, it describes the relationship between a planet’s orbital period and the size of its orbit.
To understand this law, let’s examine the meaning of “sidereal period” and “mean distance.” The sidereal period refers to the time it takes for a planet to complete one full orbit around the Sun, measured with respect to the distant stars. On the other hand, the mean distance refers to the average distance between the planet and the Sun during its orbit. By comparing the periods and average distances of different planets, Kepler discovered a consistent mathematical relationship.
Applying Kepler’s Third Law to Planetary Motion
Kepler’s third law allows us to make predictions about the orbital periods and distances of planets within our solar system. By knowing the period of a planet’s orbit, we can determine its mean distance from the Sun, and vice versa. This law provided a crucial step toward the development of accurate models for understanding and predicting planetary motion.
Let’s compare the sidereal periods and mean distances of two planets: Planet A and Planet B. According to Kepler’s third law, the ratio of the squares of their periods (PA and PB) is equal to the ratio of the cubes of their average distances (dA and dB) from the Sun:
(PA2 / PB2) = (dA3 / dB3)
Based on this equation, we can calculate the unknown values if we know at least three of the four variables (PA, PB, dA, and dB). This mathematical relationship has allowed astronomers to accurately determine the orbital periods and distances of countless planets within and beyond our solar system.
Using Kepler’s third law, scientists have made significant discoveries, such as the identification of exoplanets and the exploration of planetary systems outside our own. The law has proven to be a valuable tool in our quest to understand the universe and its vast array of celestial bodies.
In conclusion, Kepler’s third law, also known as the Law of Harmonies, provides a mathematical relationship between a planet’s sidereal period and its mean distance from the Sun. By understanding this law, astronomers can calculate and predict the orbital periods and distances of planets. This law has played a crucial role in advancing our knowledge of planetary motion and has opened up new frontiers in astrophysics and celestial mechanics. Kepler’s contributions to science continue to inspire and drive our exploration of the universe.
Significance of Kepler’s Laws
Contributions to Astronomy and Physics
– Johannes Kepler’s three laws of planetary motion represent a significant milestone in the transition from geocentrism to heliocentrism.
– These laws, developed through Kepler’s meticulous analysis of planetary motions, marked a profound step in the development of modern science.
– Kepler’s laws provided a more accurate description of the behavior of planets based on their paths through space.
– By formulating these laws, Kepler contributed to the foundation of celestial mechanics, which plays a crucial role in our understanding of the universe.
– Kepler’s work also paved the way for subsequent advancements in the field of physics, particularly in the study of gravity and motion.
Impact on Understanding the Solar System
– Kepler’s first law, the Law of Ellipses, fundamentally changed the perception of planetary orbits. It revealed that planets do not move in perfect circles around the Sun but instead follow elliptical paths.
– This law helped astronomers better comprehend the relationship between a planet and its distance from the Sun, shedding light on the concept of planetary distances.
– Kepler’s second law, the Law of Equal Areas, explained the varying speeds of planets during different parts of their orbits. It demonstrated that a planet moves faster when it is closer to the Sun and slower when it is farther away.
– This understanding of planetary speeds has significant implications for weather patterns, climate studies, and the overall dynamics of the Solar System.
– Kepler’s third law, the Law of Harmonies, established a mathematical relationship between a planet’s orbital period and the size of its orbit. This law has enabled astronomers to calculate the orbital periods of planets and predict their positions in the future.
– The accurate predictions made possible by Kepler’s laws have been invaluable in space exploration missions and the study of planets both within and beyond our Solar System.
In conclusion, Johannes Kepler’s laws of planetary motion revolutionized our understanding of the Solar System and laid the groundwork for future scientific discoveries. These laws not only explained the motion of planets but also provided a framework for advancements in astronomy and physics. Kepler’s remarkable contributions continue to shape our understanding of the universe and inspire further exploration and research.
Newton’s Laws of Motion and Planetary Motion
Connection between Newton’s Laws and Kepler’s Laws
– The Laws of Kepler for planetary motion can be derived from Newton’s Law of Gravitation. This synthesis of dynamics and astronomy accomplished by Newton provided a deeper understanding of planetary motion.
– Newton’s laws of motion, combined with the gravitational force described in his second law, imply that the planets and objects on Earth obey the same laws of motion. This unified framework allows for corrections to Kepler’s laws that are observable and applicable to all celestial objects.
– The planets, moving on ellipses as described by Kepler’s first law, are continually accelerating and experiencing a continuous force based on Newton’s laws.
Evolution of Understanding Planetary Motion
– Johannes Kepler’s three laws of planetary motion represented a significant milestone in the transition from geocentrism to heliocentrism. His meticulous analysis of planetary motions led to the formulation of these laws, which marked a profound step in the development of modern science.
– Kepler’s first law, the Law of Ellipses, revolutionized the perception of planetary orbits by revealing that planets follow elliptical paths, rather than perfect circles around the Sun. This understanding brought about a more accurate description of planetary behavior and distances.
– The Law of Equal Areas, Kepler’s second law, explained the varying speeds of planets during different parts of their orbits. This insight into planetary speeds has implications for weather patterns, climate studies, and the overall dynamics of the Solar System.
– Kepler’s Law of Harmonies, the third law, established a mathematical relationship between a planet’s orbital period and the size of its orbit. This law enables astronomers to calculate orbital periods and predict future planetary positions.
– Kepler’s laws have had a significant impact on our understanding of the Solar System, contributing to the field of celestial mechanics and providing a foundation for advancements in physics.
– The accurate predictions made possible by Kepler’s laws have been invaluable in space exploration missions and the study of planets both within and beyond our Solar System.
In conclusion, Newton’s laws of motion, combined with Kepler’s laws of planetary motion, have enhanced our understanding of the Solar System and its dynamics. Johannes Kepler’s remarkable contributions revolutionized the perception of planetary orbits and set the stage for subsequent advancements in astronomy and physics. The connection between Newton’s laws and Kepler’s laws has provided a unified framework for studying planetary motion and has paved the way for further exploration and research.
Applications of Kepler’s Laws
Predicting Planetary Positions and Orbits
– Kepler’s laws of planetary motion have been instrumental in predicting the positions and orbits of planets within our Solar System.
– By using Kepler’s laws, astronomers are able to calculate the future positions of planets with great accuracy, which is essential for planning space missions and studying celestial events.
– The ability to predict planetary positions and orbits has also been crucial in understanding the dynamics of the Solar System and how it has evolved over time.
– Kepler’s laws have allowed scientists to determine the orbits of planets and other celestial bodies, providing valuable information about their sizes, distances from the Sun, and other key characteristics.
– This knowledge has been used to develop models of the Solar System and to better understand the interactions between planets and other celestial objects.
Exoplanet Discoveries and Confirmation
– Kepler’s laws have played a pivotal role in the discovery and confirmation of exoplanets, which are planets that orbit stars outside of our Solar System.
– By observing the periodic variations in the brightness of stars, scientists can detect the presence of exoplanets and determine their orbital periods.
– Kepler’s third law, in particular, allows astronomers to estimate the size and distance of exoplanets based on their orbital period.
– Using Kepler’s laws, astronomers have confirmed the existence of thousands of exoplanets, expanding our understanding of planetary systems beyond our own.
– This has opened up new avenues of research in the search for potentially habitable planets and the possibility of finding extraterrestrial life.
In summary, Kepler’s laws of planetary motion have found practical applications in various fields of astronomy and space science. These laws enable scientists to predict planetary positions and orbits, providing valuable information for space missions and the study of the Solar System. Kepler’s laws have also been crucial in the discovery and confirmation of exoplanets, leading to advancements in our understanding of planetary systems beyond our own. These applications continue to shape our explorations of the universe and spark new discoveries in astronomy.
Modern Observations and Confirmations
Technological Advances in Confirming Kepler’s Laws
– Over the years, advancements in technology have allowed scientists to confirm Kepler’s laws of planetary motion with even greater precision.
– Telescopes and space probes equipped with sophisticated instruments have enabled astronomers to observe planetary motion and gather data in ways that Kepler and his contemporaries could only dream of.
– High-resolution imaging and spectroscopy techniques have provided detailed information about the positions, velocities, and orbits of planets in our Solar System and beyond.
– Additionally, advancements in computing and data analysis have made it possible to analyze large datasets and perform complex calculations that further validate Kepler’s laws.
Examples of Observations Supporting Kepler’s Laws
– The observations of Jupiter’s moons made by Galileo Galilei in the 17th century provided early evidence for the validity of Kepler’s laws.
– By tracking the moons’ positions over time, Galileo observed that they followed elliptical orbits around Jupiter, as predicted by Kepler’s first law.
– Modern observations of the planets in our Solar System, such as the Cassini mission to Saturn, have continued to support Kepler’s laws.
– These observations have revealed the intricate dynamics of planetary systems, including the gravitational interactions between multiple planets and their moons.
– The discovery of exoplanets using the transit method has also provided compelling evidence for the accuracy of Kepler’s laws in predicting the orbits of planets orbiting other stars.
In conclusion, modern technological advancements have allowed scientists to confirm and refine Kepler’s laws of planetary motion. Through high-resolution observations and sophisticated data analysis, astronomers have provided numerous examples supporting the accuracy of Kepler’s laws. These observations not only validate the work of Kepler but also deepen our understanding of the dynamics of planetary systems within and beyond our Solar System. Additionally, the discovery of exoplanets using Kepler’s laws has opened up new avenues of research and sparked further exploration into the possibility of finding habitable planets and extraterrestrial life.
Criticisms and Challenges to Kepler’s Laws
Alternate Theories in Planetary Motion
– While Kepler’s laws have been successful in predicting planetary positions and orbits, they have faced criticism and alternative theories over the years.
– One such theory was proposed by French mathematician and astronomer Pierre-Simon Laplace, who suggested a modification to Kepler’s second law.
– Laplace’s theory proposed that the planets move in slightly elliptical orbits with the Sun located at one of the foci, in contrast to Kepler’s claim that the Sun is located at the center of the ellipse.
– Another alternative theory was put forth by German mathematician Carl Friedrich Gauss, who suggested that the gravitational force between the Sun and the planets is variable and not constant as proposed by Kepler.
– Gauss’s theory aimed to explain the discrepancies observed in the positions of the planets, particularly in explaining the irregularities in the motion of Mercury.
Limitations and Adjustments to Kepler’s Laws
– While Kepler’s laws have been very successful in predicting planetary positions, they are not entirely accurate and require adjustments in certain cases.
– For example, Kepler’s laws assume that planets orbit around a stationary Sun, but in reality, both the Sun and the planets are in motion due to the gravitational interactions with each other.
– This motion of the Sun and the planets can cause slight deviations from the ideal elliptical orbits predicted by Kepler’s laws.
– Additionally, Kepler’s laws do not account for the gravitational influences of other celestial bodies, such as moons or nearby planets, which can perturb the orbits and lead to deviations from the predicted positions.
– To overcome these limitations, astronomers have developed more complex mathematical models and techniques, such as perturbation theory and numerical integration, to accurately predict planetary positions and account for the gravitational interactions with other bodies in the Solar System.
In conclusion, while Kepler’s laws of planetary motion have been successful in predicting planetary positions and orbits, they have faced criticism and alternative theories. Scientists have proposed modifications and adjustments to Kepler’s laws to account for the limitations and improve the accuracy of predictions. These advancements in understanding planetary motion have contributed to our knowledge of the dynamics of the Solar System and have paved the way for further discoveries in astronomy and space science.
Criticisms and Challenges to Kepler’s Laws
Alternate Theories in Planetary Motion
– Kepler’s laws, although successful in predicting planetary positions and orbits, have faced criticism and alternative theories from astronomers and mathematicians.
– French mathematician and astronomer Pierre-Simon Laplace proposed a modification to Kepler’s second law. He suggested that planets move in slightly elliptical orbits with the Sun located at one focus, contrary to Kepler’s claim that the Sun is located at the center of the ellipse.
– German mathematician Carl Friedrich Gauss proposed another alternative theory. He suggested that the gravitational force between the Sun and the planets is variable and not constant, as proposed by Kepler. Gauss aimed to explain the discrepancies observed in the positions of the planets, particularly the irregularities in the motion of Mercury.
Limitations and Adjustments to Kepler’s Laws
– While Kepler’s laws have been successful in predicting planetary positions, they are not entirely accurate and require adjustments in certain cases.
– Kepler’s laws assume that planets orbit around a stationary Sun, but in reality, both the Sun and the planets are in motion due to gravitational interactions. This motion can cause slight deviations from the ideal elliptical orbits predicted by Kepler’s laws.
– Additionally, Kepler’s laws do not account for the gravitational influences of other celestial bodies, such as moons or nearby planets. These influences can perturb the orbits and lead to deviations from the predicted positions.
– To overcome these limitations, astronomers have developed more complex mathematical models and techniques. Perturbation theory and numerical integration, for example, have been used to accurately predict planetary positions and account for the gravitational interactions with other bodies in the Solar System.
Conclusion
In conclusion, Kepler’s laws of planetary motion have faced criticisms and alternative theories, but they have also been a foundation for understanding the dynamics of the Solar System. Despite their limitations, adjustments and advancements in mathematical modeling and techniques have improved the accuracy of predictions. These developments have contributed to our knowledge of planetary motion and have paved the way for further discoveries in astronomy and space science.
Summary of Kepler’s Laws of Planetary Motion
– Kepler’s first law states that planets move in elliptical orbits with the Sun located at one focus of the ellipse.
– Kepler’s second law states that a planet covers equal areas in equal times, meaning it moves faster when it is closer to the Sun and slower when it is farther away.
– Kepler’s third law shows a precise mathematical relationship between a planet’s distance from the Sun and the time it takes for the planet to revolve around the Sun.
Lasting Impacts and Future Research Directions
– Kepler’s laws of planetary motion have provided a framework for understanding the behavior of planets and other celestial bodies in the Solar System.
– The laws have paved the way for advancements in astronomical observations and the development of more accurate models to predict planetary positions.
– Future research will continue to refine our understanding of planetary motion, incorporating factors such as the influence of other celestial bodies and gravitational interactions.